Estimates of an integral operator
Abstract
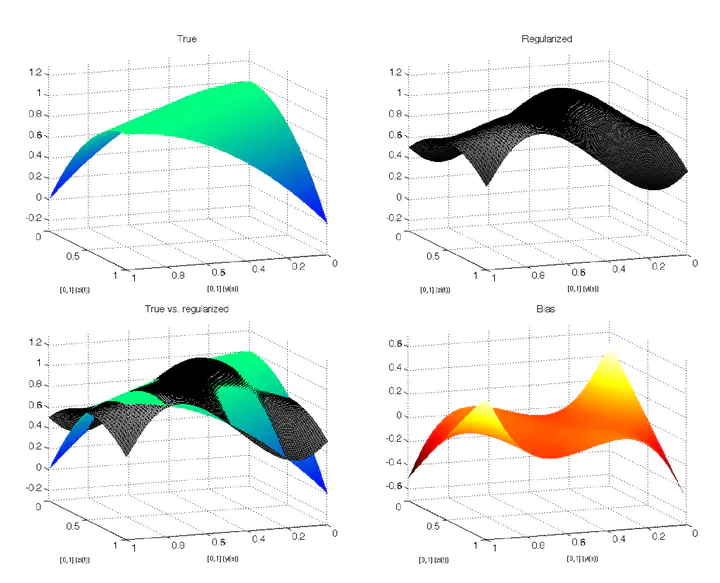
In this paper, we develop new estimation results for functional regressions where both the regressor and the response are functions of Hilbert spaces, indexed by the time or a spatial location. The model can be thought as a generalization of the multivariate regression where the regression coefficient is now an unknown operator . We propose to estimate the operator by Tikhonov regularization, which amounts to apply a penalty on the norm of . We derive the rate of convergence of the mean-square error, the asymptotic distribution of the estimator, and develop tests on . As trajectories are often not fully observed, we consider the scenario where the data become more and more frequent (infill asymptotics). We also address the case where is endogenous and instrumental variables are used to estimate . An application to the electricity consumption completes the paper.
